우리가 어떤 알고리즘이 더 나은 알고리즘인지 판단할 수 있는 척도는 무엇일까?
흔히 고려해 볼 수 있는 사항은 다음과 같다.
- 실행시간
- 코드의 길이
- 자주 발생하는 작업/연산의 수(소팅에서의 비교 연산)
그러나, 코드가 길다고 해서 실행 시간이 짧다는 보장이 없을 뿐더러, 실행시간의 경우에는 하드웨어의 차이에 따라
그 결과가 달라질 가능성이 높다고 볼 수 있다. 그렇다면, 우리는 어떤 기준을 가지고 이를 판단해야 할까.
시간복잡도
시간복잡도란, 이 중 필요한 단위연산을 기준으로 하는 복잡도를 의미하며,
알고리즘이 한 번 수행되는 동안 수행되는 단위연산의 수를 중심으로 비교한다.
이 단위연산은 해당 알고리즘에서 가장 많이, 필수적으로 수행되어야 하는 연산을 말한다.
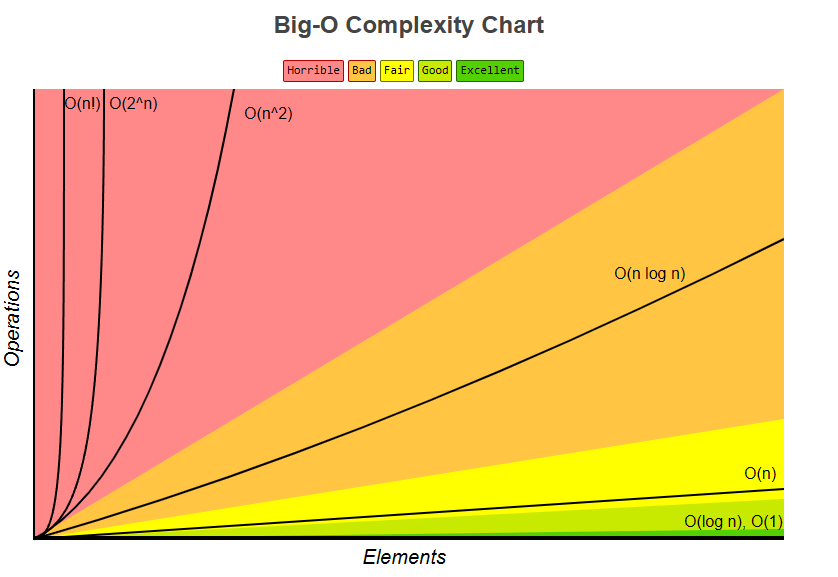
보통 시간복잡도를 표현하기 위해 가장 많이 사용하는 표기법은 Big-O-Notation(빅오 표기법)이다.
Big-O-Notation
Big-O 표기법은 문제의 문제의 수행시간에 대한 함수의 표현식으로
문제의 크기에 비례하여 가장 빠르게 증가하는 연산에 관련된 함수로 표현하는 것을 의미한다.
이 함수를 "복잡도 함수"라고 부르며, 이 복잡도 함수가 작을수록 더 나은 알고리즘임을 의미하는 표기 방식이다.
보통 O(f(n))형태로 표현하며, 이 f(n)이 복잡도 함수이고,
연산수가 무한으로 증가한다면 최고차항의 수만 살펴보면 되기 때문에 보통 최고차항의 차수를 중심으로 판단한다.
'알고리즘 스터디' 카테고리의 다른 글
| 이것이 코딩테스트다 챕터 6 정렬 (0) | 2024.05.20 |
|---|---|
| 이것이 코딩테스트다 챕터 5 DFS/BFS (0) | 2024.05.13 |
| 이것이 코딩테스트다 챕터 4 구현 (0) | 2024.05.06 |
| 코드업 기초 100제 51~98 (0) | 2024.04.08 |
| 파이썬 기본 문법 <조건문,반복문> (0) | 2024.03.31 |